论文阅读:Optimally Combining Sampling Techniques for Monte Carlo Rendering —— 一文读懂MIS
论文阅读:Optimally Combining Sampling Techniques for Monte Carlo Rendering
中文翻译大概叫“对蒙特卡洛渲染中复合采样技术的优化”,从源头说起,一文搞懂mis(multiple importance sampling)多重重要性采样是什么为什么怎么样,以及为什么glsl-pathtracer要对反射方向以及光源都采样一次。
介绍
渲染就是积分,积分很多都用MC(蒙特卡罗方法),但是MC的缺点就是因为他是基于概率估计,估计结果会有方差,具体体现在图像上就是噪声。
因为计算机图形学中的积分函数往往是病态的,所以我们经常需要不止一种采样策略来让我们的方差变小。
因此,这里需要解决的问题就是——我有很多种采样方法,如何调整每种采样方法的权重,来使最终的计算方差最小。“我们方法的意义不在于我们可以采用几种糟糕的采样技术并从中炮制出一种好的技术,而是我们可以采用几种可能好的技术并将它们结合起来,以便保留每种技术的优势”
第二部分,我们回顾了用于渲染的 MC 集成的基础知识,并给出了一个例子来激发我们的方差减少框架。
第三部分解释了我们关于组合来自多个分布的样本的想法,并在多个模型下给出了理论依据(证明)
第四部分,我们展示了几个应用领域的计算图像和数值结果:面光源的光泽高光、一些光能传递算法的“最终聚集”通道,以及使用双向路径追踪直接求解渲染方程
第五部分讨论了与我们的工作相关的一些权衡和未解决的问题
2.1 Monte Carlo rendering
回顾了两个问题,三点渲染和蒙特卡洛积分。
三点渲染:
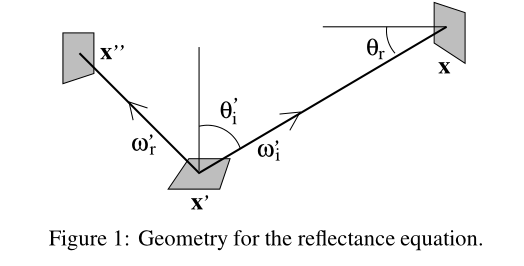
也就是经典的渲染方程
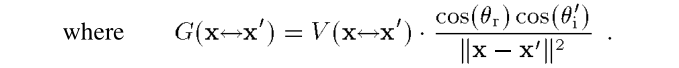
这里的L是对出射radiance的度量,我们可以用很多种很多种L的度量结果,再将其加权起来,就是$I_p$
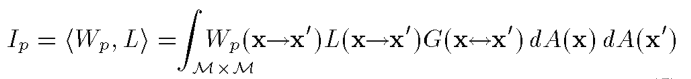
这里其实不重要。
2.2 蒙特卡洛积分:
首先是蒙特卡洛积分是什么?
蒙特卡洛积分 - 知乎 (zhihu.com)这篇文章讲的很好。
大概讲起就是处理一类很难算出解析式(或者压根不知道解析式)的函数的积分的一种方法。具体做法就是用一个概率分布来对函数进行采样,用采样的结果除采样的概率,再将其加和平均,得到所求积分的估计值。
所求积分:这里的$\mu$是对x的一种measure
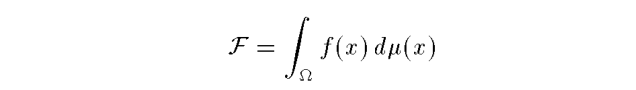
积分的估计值:
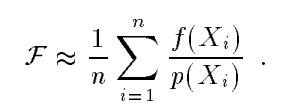
相应的这种算法虽然是一种无偏估计(期望和所求积分相同),但是有方差,而且方差随采样数量$n$的增加以$\frac{1}{n}$的速度减小。
方差:这里的$F$是$f(X)/p(X)$
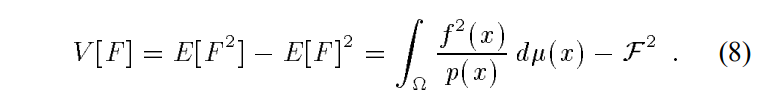
如果这里的每个采样结果都是独立同分布的,如果将所有此采样结果加权平均,明显最终的方差就是每个F方差的$\frac{1}{n}$。所以要想方差小,就要付出更多的时间来采更多的样本。
但是这里也能看到,方差和我们设计的采样的概率密度函数密切相关。如果我们换一种思路:设计采样的分布函数,从而降低单个$V[F]$。这样也能让整个方差降下来。很明显,当$p=\frac{f}{\mathcal{F}}$,方差就没了。但我们不知道$\mathcal{F}$。
一个结论:如果使用蒙特卡洛积分的概率密度函数和f本身很像,得出的积分的方差就会很小。故将函数本身作为pdf来采样收敛的更快。此之谓重要性采样。
2.3 给出了一个例子——glossy highlights
回顾刚才讲的三点渲染,也就是说要计算从x’出发射到x’’的光的radiance。
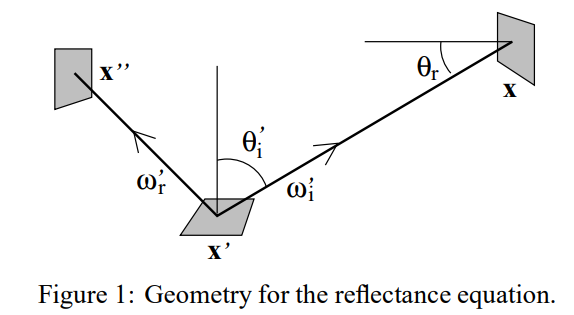
而一个渲染方程的积分式可以是两种不同的形式,分别是根据x’立体角的不同方向进行积分,以及根据场景不同位置点x给x’的flux进行积分:
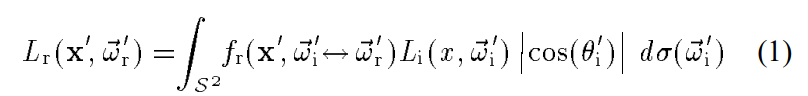
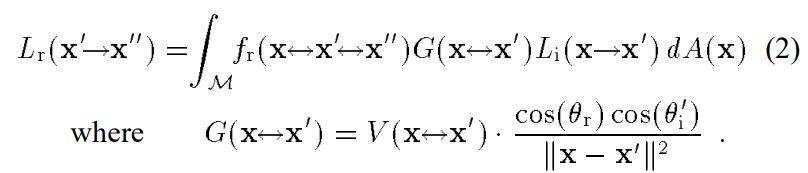
(后者的A是对x点对应的小表面面积的衡量。)
这里依据两种积分,引出了两种不同的采样方式,并用两张图表示了两种不同采样方式的缺点。图片中四种光源的照射强度相同从左到右面积越来越大,四种地板从上到下越来越粗糙。

第一种:从渲染方程(2)版本引出的依据光源进行采样。
首先明确一点,目前只考虑一次反射,也就是忽略由于光反射形成的光顶点作为光源的情况。渲染方程2的原理就是,对于每个发光的表面进行积分,最后得出点从各个发光表面传来的光的总和。
因为我们用的是蒙特卡罗方法,因此处理这个积分实际上使用的是采样的方式。也就是,从所有的发光表面上采一个点,然后用这个点和一个概率系数相乘得到积分的估计值。这部分对应于GLSL-PathTracer的Sample one light部分。
从图中可以看出来,这种采样方法对于表面越平滑、光源越大的情况,越是失真。最需要看两个对比:
- 最光滑表面上的粉光和蓝光——首先由于根据光源采样,四个光源选一个,这就对蓝光实际上“不公平”。其次光源面积越大,光的发射方向越多,对于光滑表面越可能不会射到眼睛位置。
- 蓝光在最粗糙和最光滑表面的对比——要从光源采出一条出射光线。这条光线对于光源来说,光源面积大,这束采到的蓝光的位置可能就不太会是本应该反射的光源位置。由于BRDF很可能射的很偏,在渲染方程中对应的就是G值越小。而表面越粗糙,BRDF对偏向光的接受程度反而更高了,所以看起来要和粉光差不多。
这看起来是采样方式的问题——这里是按照光源点flux的贡献进行采样的,看起来对面积大光源不公平。但如果对于面积大但是贡献少的光源采样多的话就变成了有偏估计,更不科学。总之这种采样方式对于光滑且光源面积大的情况的估计的方差很大。

第二种:从渲染方程(1)版本进行依据方向角(BRDF)的采样
这种采样方式就是相当于以x’点为中心,从各个方向角反向追溯可能来自光源的方向,然后依据BRDF选择一条最可能的方向,将这个方向传来的flux作为蒙特卡罗方法的估计值。
这里更可以看出这种方式也会产生问题。最糟糕、方差最大的情况就是小光源+粗糙表面。这里也简述一下原因:
- 光源越小:意味着我从x’依据BRDF采样出的决定性光线越有可能打不到本应该打到的光源。光源面积小了概率就小了。这一点在光滑表面尚不明显,因为这些本应该被光源照亮的决定性光线的确就是想要的来自光源的光线。
- 表面越粗糙:显然,采样的BRDF在分布上更平均了,本来光源就小,这下更不太可能碰到光源了。采出来的要么根本就是到处乱射,要么运气好碰到光源之后变得贼亮。
之后他用两种方法进行了结合,使用具有的幂启发式计算来自(a)和(b)的样本的加权组合。
两种采样方式都属于重要性采样,只不过一种是直接采样一个点x,另一种是根据采样到角度进一步根据这个角度光线的first hit point得出x。两种采样的概率关系:
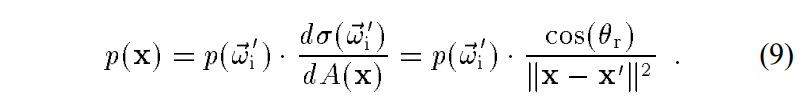
2.4 作者在这里开始讲他的减少方差框架(Framework of variance reduction)
首先,设计一组重要抽样分布p1,…,pn。对于f可能较大的每个区域,我们尝试构建一个采样分布,在该区域上很好地近似f。这些分布的一个很好的来源是上面的例子,其中f是几个不相关函数的乘积,每个pi与这些函数的一个子集的乘积成正比。
接下来,我们确定从每个pi取多少个样本。我们假设这是预先确定的,基于f和pi的知识。
最后,将积分估计为所有样本值的加权组合。本文的主要课题是如何做到这一点,使估计是无偏的,具有低方差。
3 Combining sampling techniques
第三部分讲的是如何结合很多种sample方式,使得得到的蒙特卡洛积分的方差最小。
设计了一套符号系统:$f$是被积函数integrand,$p_1,…,p_n$分别是n种采样方式的概率密度函数。我们只能知道两个事情:给一个x,求f(x),或者求pi(x)。这里又定义了一个ci,表示的是第i种分布抽到的样品数占所有抽样总数的比例。注意ci的总和为1,ci表示每种分布的权重(很明显ci不能反映具体每个样品占全部样品总数的权重比,ci只与抽样分布i有关,与抽样结果f(x)以及x本身无关)
引入ci之后,可以据此得出样品x在所有抽样方法中出现的概率:$\bar{p}(x)=\sum_ic_ip_i(x)$。至于具体怎么设计ci,作者说在后面谈。
3.1 The combined sample distribution
用这个新的$\bar{p}$作为combine了所有抽样方法的新的概率密度函数,就形成了 the balance heuristic 方法 (平衡启发式)。个人理解,平衡代表着每个抽样样本在所属分布中的概率不受其他分布影响,启发式代表,嗯这是一种启发式的方法。
3.2 The multi-sample model
这里作者定义了combined estimator的广义模型
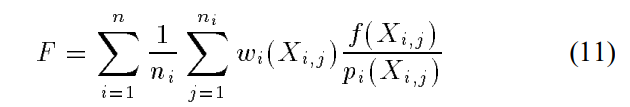
这里的i表示的是第i种分布,这里的j表示的是在第i个分布中的第j个抽样结果。
通过设计函数wi(这里一共是n个函数,每种分布都要有一个w),来让这个F的方差最小。本质上还是优化问题,自变量是f和几种分布p,参数是w,优化目标是F的方差。
为了让我们的估计是无偏估计(unbias),还需要在w的解空间加一个限制条件:$\sum_iw_i(x)=1$。于是无偏:
注意到这里的解空间相当自由,比上面说的ci的情况自由得多。
3.3 The balance heuristic
我们把这里的wi定义为以下形式:
这时我们的F就是:
我们称之为the balance heuristic。之所以叫heuristic,因为这是一种启发式地确定w解空间的方式。后面还有很多种类似方法。
此时把这种F设为$\bar{F}$。有结论:告诉我们 the balance heuristic 为什么能,为什么好。因为方差确实小。
作者在Appendix里面还给出了证明,自己看吧。
3.4 Other weighting heuristics
作者还提出了几种其他heuristics:

glsl-pathtracer里面用的就是这种mis方法:
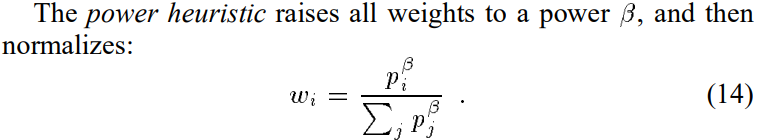
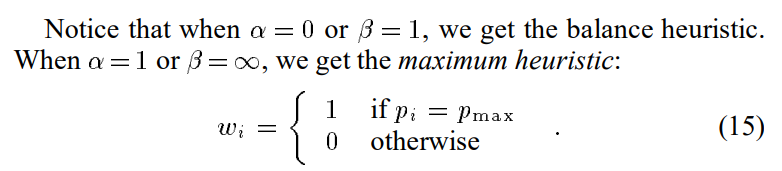
这些方法的特点在于:一种p比其他的p表现更好的时候能显著减少方差。
3.5 The one-sample model: optimality
这里作者对一次采样模型下的最优解进行了一个论述:
在这个一次采样模型下,每次采样都是随机地产生自$p_i$,而分布$p_i$被以概率$c_i$选择。(这也就是路径追踪的情况)
其次,每个蒙特卡洛积分估计器都是被一个权重的集合{w(x)}参数化。
选择采样分布、采样、计算经过权重调整后的采样值,这三步过程可以被我们的combined estimator数学地表示为:
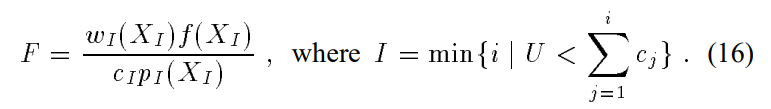
这里的U,是一个从$[0,1)$上均匀分布的随机变量,用来产生I,I的意义是:按照每个分布占总体比例的权重随机采样,采到的分布的index。
$X_I$是I里面采样出的一个值。如果所有wi项的加和为1,就说明这个估计是一个无偏估计。在这种情况下,使用 balance weighting strategy 是最优的:

4 Experiments
这部分是他做的实验。
4.1 Distribution ray tracing
4.2 Final gather
4.3 Bidirectional path tracing
5 Discussion
。。。TBD
5.1 Conclusions
5.2 Choosing the number of samples
5.3 Comments on direct lighting
。。。




