读 Relighting Humans 论文
读 Relighting Humans 论文
[TOC]
基本思想
记下来。不然时间长又忘了。
首先说一下这篇论文想解决的问题:现有relight方法对于阴影遮挡这部分的无力。
之前的方法都是使用球谐函数直接照明而忽略了遮挡问题,导致一些比如说腋窝等部位异常明亮。但实际上这些部位由于大部分被自身遮挡,不应该出现过多的明亮现象。
实际上不是之前的人不想解决这个问题,而是考虑这个问题之后会使计算变得很复杂。回顾 irradiance 的方程:
$$
E(\textbf{n})=\int_{\Omega(\textbf{n})}L(\omega_i)V(\omega_i)max(\textbf{n}\cdot \omega_i, 0)\mathrm{d}\omega_i
$$
对于一个shading point,这里面,n是其单位法向量,omega指的是方向角,L就是对应角度传来的radiance,后面的点乘表示的是一个余弦衰减系数。V是visibility项,表示这个方向是否被遮挡。对于每个shading point来讲,如果不考虑V term,计算相对容易。实际上用prt加上V term,这个计算也可以接受。不能接受的是这个V怎么算出来。目前就是使用从shading point向四面八方采样的方法,但采样很昂贵。所以之前干脆用不含V的公式
$$
E(\textbf{n})=\int_{\Omega(\textbf{n})}L(\omega_i)max(\textbf{n}\cdot \omega_i, 0)\mathrm{d}\omega_i
$$
对于relight的渲染过程,之前的方法是把L和cos项分解成球谐函数(SH),然后通过球谐基函数和系数点乘算出结果(PRT方法)。这里用向量代表基函数和系数。T就是系数,L就是SH基函数:
$$
E=\textbf{T}^{T}\textbf{L}
$$
当然这个系数和基函数里面是不包括V term的。网络的话也是输入一张图片,输出得到反射率图(albedo)光照图和不含V term的光通量图。这个光通量图对应的就是上面公式里的系数向量T。
现在的作者想能不能我假装公式里有V term,但我不算这个V term,我让他来学这个V怎么算,从而弄出带遮挡的效果。作者原本怀疑自己的数据集不足以让网络学出来,但是貌似结果还不错。
大概是这样。
损失函数:
先说明一下符号:
$$
\mathcal{D_H}: 人图像数据。包括以下内容:
$$
$$
\mathbf{M}^c_j\in {0,1}^{N\times c}: 人图像的\alpha 遮罩,c表示通道数,j是图片数,N是像素数
$$
$$
\Lambda_j\in\mathbb{R}^{N\times 3}: albedo图,3对应RGB
$$
$$
\Psi_j\in\mathbb{R}^{N\times 9}: 光传输矢量(transport)图,9对应3阶SH的一共九个基函数
$$
$$
\mathcal{D_L}: 光(light)的数据。包括以下内容:
$$
$$
\Pi_k\in\mathbb{R}^{9\times 3}:环境光照,9对应SH,3对应RGB
$$
以上都是输入,要的就是给DH和M,推断出albedo、light和transport。其中Lambda、Psi和Pi都是Ground Truth,推断出的Lambda、Psi和Pi都要在字母上面加个波浪线。另外后面的M操作都被忽略了。
最后要根据从第j张图像和第k种光照中重建出来的图实际上就是算出:
$$
\tilde{I}{j,k}=\tilde{\Lambda}{j,k}*(\tilde{\Psi}{j,k}\tilde{\Pi}{j,k})
$$
这里用到了15种损失函数,其中四种借鉴自SfSNet,另外十一种都是作者自己加的。总损失函数就是所有的损失加起来,很粗暴。
SfSNet的四种是:
- Lambda的L1 Loss
- Pi的L1 Loss
- Lambda、Psi、Pi乘积的L1 Loss
- Psi的L2 Loss
作者加的十一种,都是L1 Loss:
- Lambda和Psi的L1 TV Loss(total variation loss),共两种
- (带下划线表示infer出的,不带的表示GT)~Psi和Pi、~Pi和Psi、~Psi和~Pi的L1 Loss,都是相比于Pi和Psi来说。共三种
- (带下划线表示infer出的,不带的表示GT)都是相比于 Lambda*Psi*Pi的结果,共六种。具体哪六种太多了自己看吧。
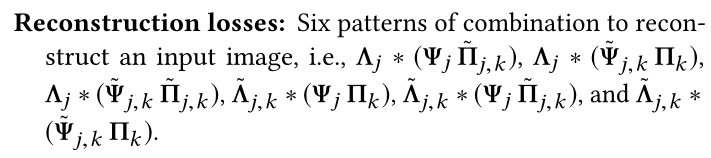
最后,什么是L1 Loss:
$$
L=\sum|y-f(x)|
$$
什么是L2 Loss:
$$
L=\sum(y-f(x))^2
$$
模型结构
jh那里写的很清楚了。



